1. 多元系原子間ポテンシャル
原子挿入法に基づいた単元系の原子間ポテンシャルが与えられた条件下での,多元系合金の原子間ポテンシャルの表式を導出する.
原子挿入法によると結晶の全エネルギーは
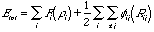 (1)
(1)
で与えられる.ここで,Fi(ri)はi番目の原子位置における電子密度riに対する原子挿入関数であり,fij(Rij)は距離Rij離れたi-j原子間の静電エネルギーである.和は結晶を構成する全原子N個について行う.Fi(ri)を平均電子密度reのまわりで2次の項までテーラー展開すると,全エネルギーは
 (2)
と近似できる.ここで,fj(Rij)はj番目の原子がi番目の原子位置に与える電子密度,rはre/NであるがNが十分大きいので無視できる.また,3体間相互作用項は無視した.第1項は,iだけの関数であるので,第2項の[
] 内は原子挿入法における原子間ポテンシャルVij(Rij)である.i番目とj番目が同種原子,例えばA原子のとき,
(2)
と近似できる.ここで,fj(Rij)はj番目の原子がi番目の原子位置に与える電子密度,rはre/NであるがNが十分大きいので無視できる.また,3体間相互作用項は無視した.第1項は,iだけの関数であるので,第2項の[
] 内は原子挿入法における原子間ポテンシャルVij(Rij)である.i番目とj番目が同種原子,例えばA原子のとき,
 (3)
となる.異種原子の場合,
(3)
となる.異種原子の場合,
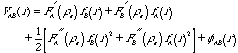 (4)
となる.
(4)
となる.
多元系合金において,(3)(4)式中のF'A(re),fA(r)などのパラメーターを決定することは困難である.その理由は,多くの場合これらのパラメーターを決定するために必要な合金の物性データーが十分に得られていないことである.そこで,本研究ではこれらのパラメーターを単元系で得られた原子挿入関数および電子密度を用いることとした.しかし,原子挿入関数が既知としても,(3)(4)式中の多元系合金における平均電子密度reは未知である.そこで,本研究ではさらに各構成原子の単元系における平均電子密度により近似したところ,
(4) 式は
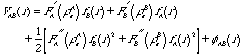 (5)
となる.また,fABはfAAとfBBの幾何平均で近似する.こうすることにより多元系合金に関するデーターがない場合でも原子間ポテンシャルを決定することが可能となる.
(5)
となる.また,fABはfAAとfBBの幾何平均で近似する.こうすることにより多元系合金に関するデーターがない場合でも原子間ポテンシャルを決定することが可能となる.
2. 合金の固溶熱
合金の全エネルギーをEtotalloy,単元系のそれをEtotIとすると,合金の1原子当たりの固溶熱は,
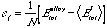 (6)
で与えられる.〈〉は,合金の組成に対する平均を意味する.(2)式の展開を用い,さらに平均電子密度に各構成原子の単元系におけるそれを用いると,(2)式第1項の挿入関数の項は相殺されるので,(6)式は
(6)
で与えられる.〈〉は,合金の組成に対する平均を意味する.(2)式の展開を用い,さらに平均電子密度に各構成原子の単元系におけるそれを用いると,(2)式第1項の挿入関数の項は相殺されるので,(6)式は
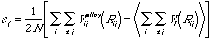 (7)
となる.
(7)
となる.
不規則合金の場合,構成原子の配列はランダムであるので,(7)式第1項を平均原子間ポテンシャルValloyを用いて,
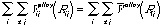 (8)
と近似する.平均原子間ポテンシャルはもはや原子の種類に依存しないので(7)式は
(8)
と近似する.平均原子間ポテンシャルはもはや原子の種類に依存しないので(7)式は
 (9)
となる.ここで,RmIはI番目の構成原子の単元系における原子間距離を示す.また,mについての和はR0=0を除くものとする.2元系不規則合金の場合,
(9)
となる.ここで,RmIはI番目の構成原子の単元系における原子間距離を示す.また,mについての和はR0=0を除くものとする.2元系不規則合金の場合,
 (10)
であり,さらに原子間に相関がないとするとValloyは
(10)
であり,さらに原子間に相関がないとするとValloyは
 (11)
と近似できる.
(11)
と近似できる.
3. 弾性定数
弾性定数は,(1)式で表される結晶のエネルギーの無限小ひずみに対する平衡状態での2階偏導関数により
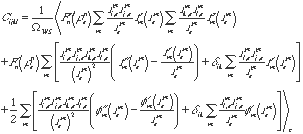 (12)
(12)
と与えられる.ここで,WWSは1原子あたりの体積であり, は配置平均を示す.
は配置平均を示す.
4. ポテンシャルパラメーターの決定
単元系EAMポテンシャルを格子定数a,体積弾性率B,せん断弾性率G,凝集エネルギーEc,空孔の形成エネルギーEvの実験値を再現するように決定した.電子密度関数f(r),静電相互作用f(r)はOhとJohnsonの方法(D.J.Oh and R.A.Johnson: J.Mater.Res., 3 (1988), 471-478.)に基づき次のように指数関数近似した.

(13)
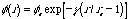
(14)
ここで,
reは最近接原子間距離である.
![]() (1)
(1)![]() (1)
(1) (2)
(2)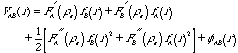 (4)
(4)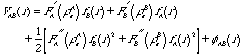 (5)
(5)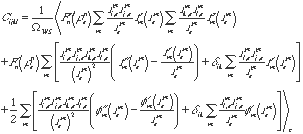 (12)
(12)
![]() は配置平均を示す.
は配置平均を示す.
![]()
![]()